A derivative is a financial instrument whose price is derived from an underlying asset. Thus, in very simple words, the price and value of a derivative stem from its underlying asset. The underlying asset can be anything that has some value. The most common forms of derivatives are forwards, futures, options, and swaps. Although other derivatives also exist, known as exotic derivatives, in this article we will focus on these four types of derivatives.
Although the pricing models differ for each type of derivative, the underlying principle is the same: financial derivatives are priced based on non-arbitrage principle, or the law of one price.
Forward Contracts
A forward contract is a private agreement between two parties giving the buyer an obligation to purchase an asset, and the seller an obligation to sell an asset at a set price at a future point in time. The underlying asset can be anything of value. In order to understand this better, let us look at a simple example.
Let us assume that the underlying asset here is a 10 kg bag of apples that have not been harvested yet. Technically, the underlying asset does not even exist, so it has no financial value. However, it is still possible to assign a price to it. Suppose that a farmer enters into a forward contract to sell the 10 kg bag of apples at a price of $20 in 3 months' time when the apples will be harvested. The farmer does this because he fears that the price of apples may go down in the future, resulting in a loss for him. So in order to set off or hedge the potential loss, the farmer enters into a forward contract with a buyer who agrees to buy the 10 kg bag of apples at the $20 price determined today. This means that 3 months from now, the forward contract will be executed at $20 regardless of the price in the future. In this manner both the buyer and seller transfer the risks to each other.
Forward contracts are often customized and trade over the counter.
Future Contracts
A futures contract is a legal agreement to buy or sell a particular commodity, or security at a predetermined price at a specified time in the future. Futures contracts are standardized for quality and quantity in order to facilitate trading on an organized exchange. In addition, unlike forwards, the profit and loss of a futures contract is settled daily.
Despite the differences, the underlying principles for both futures and forwards are the same. The parties enter into a contract to buy or sell a particular underlying asset at a fixed price in the future, and the value of the contract is determined as the underlying asset is realized.
Option Contracts
An options contract is an agreement between a buyer and seller that gives the buyer of the option the right but not the obligation to buy or sell a particular asset at a later date at an agreed-upon price. Options contracts are often used in securities, commodities, and real estate transactions.
In principle, options are similar to forwards and futures but the difference is its holder has a right, but not an obligation to buy or sell the underlying asset. A call option gives the buyer the right to buy the asset at a predetermined price at or before maturity. A put option allows the holder to sell at a predetermined price at or before expiration.
Going back to our original example, suppose that the farmer has bought a put option that allows him to sell apples at $20. Three months later, if the price of 10 kg bag of apples becomes $24, then in this situation the farmer would have the option of not executing the contract at $20 and instead of selling the 10 kg bag of apples at the market price of $24. However, if the price of the apples falls down to $15, then the farmer can exercise the put option and sell the apples at the contractual price of $20.
Black-Scholes option pricing model
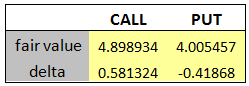
There are different models for valuing options. The earliest model is called the Black-Scholes option pricing model which provides an analytical, closed-form formula for valuing a European option. The model requires 5 important input parameters: spot price, strike price, volatility, risk-free rate, maturity.
Binomial option pricing model
Binomial option model is used to value American style options. The model relies on the assumption that for the next time period, a stock can move up, or down with certain probabilities. The major advantage of the binomial model is that it’s relatively simple. To value an option using this method, a tree of possible values of the underlying assets is built first. Then the option value is determined by calculating its payoffs at maturity and rolling back to time zero.
Swaps
A swap is a derivative contract through which two parties can exchange the cash flows or liabilities from two different financial instruments. The most common type of swap is interest rate swap, however, there exist other types such as commodity and currency swaps.
Interest rate swaps are used to manage and transfer interest rate risks. Let’s take a look at an example, a parent company operating in the USA has a subsidiary in Europe. The parent in the USA has to pay a fixed-rate loan in dollars whereas the subsidiary based in Europe has to pay a variable rate loan in Euro. The parent wants to pay a variable rate based on its cash flow situation whereas the subsidiary wants the fixed-rate loan because of the certainty of payments. Thus, both the parent and subsidiary will enter into an interest rate swap where the parent will end up paying the variable-rate euro loan and the subsidiary will end up paying the fixed-rate dollar loan.
An interest rate swap can be valued by decomposing it into fixed-rate and floating-rate bonds. Essentially, the value of each leg is determined by calculating the Net Present Value of future cash flows. An alternative way to value an interest rate swap is to view it as a series of Forward Rate Agreements.
Article Source Here: Derivative Pricing and Valuation
![]()
![]()