A Simple Hedging System with Time Exit

This post is a follow-up to the previous one on a simple system for hedging long exposure during a market downturn. It was inspired by H. Krishnan’s book The Second Leg Down, in which he referred to an interesting research paper [1] on the power-law behaviour of the equity indices.  The paper states,

We find that the distributions for ∆t ≤4 days (1560 mins) are consistent with a power-law asymptotic behavior, characterized by an exponent α≈ 3, well outside the stable Levy regime 0 < α <2. .. For time scales longer than ∆t ≈4 days, our results are consistent with slow convergence to Gaussian behavior.

Basically, the paper says that the equity indices exhibit fatter tails in shorter time frames, from 1 to 4 days. We apply this idea to our breakout system.  We’d like to see whether the 4-day rule manifests itself in this simple strategy. To do so, we use the same entry rule as before, but with a different exit rule.   The entry and exit rules are as follows,

Short at the close when Close of today < lowest Close of the last 10 days

Cover at the close T days after entry (T=1,2,... 10)

The system was backtested on SPY from 1993 to the present. Graph below shows the average trade PnL as a function of number of days in the trade,

[caption id="attachment_350" align="aligncenter" width="485"]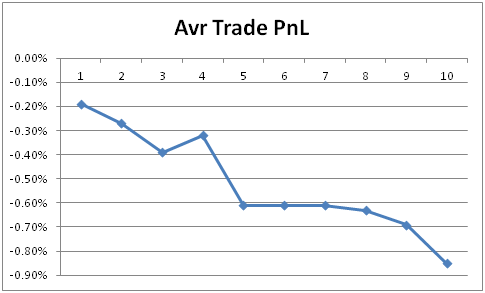 Average trade PnL vs. days in trade[/caption]

We observe that if we exit this trade within 4 days of entry, the average loss (i.e. the cost of hedging) is in the range of -0.2% to -0.4%, i.e. an average of -0.29% per trade. From day 5, the loss becomes much larger (more than double), in the range of -0.6% to -0.85%. The smaller average loss incurred during the first 4 days might be a result of the fat-tail behaviour.

This test shows that there is some evidence that the scaling behaviour demonstrated in Ref [1] still holds true today, and it manifested itself in this system.  More rigorous research should be conducted to confirm this.

 References

[1] Gopikrishnan P, Plerou V, Nunes Amaral  LA, Meyer M, Stanley HE, Scaling of the distribution of fluctuations of financial market indices, Phys Rev E, 60, 5305 (1999).

Read Full Article Here: A Simple Hedging System with Time Exit

Historical Default Rates Do Not Predict Future Defaults

Yesterday, Bloomberg published an article arguing that the current credit risk is low because the default rate is low,

Insulated by cheap money from the QE era and bolstered by cash on their balance sheets, it remains rare for companies in Europe and the U.S. to miss debt payments. Among higher-risk speculative-grade firms the default rate fell to 2.9 percent last quarter, and may drop further to 2.1 percent by year-end, according to Moody’s Investors Service. And only one investment-grade firm has defaulted since 2012, data from Standard & Poor’s Global Ratings show.

“Default rates are on the floor,” said Fraser Lundie, co-head of credit at Hermes Investment Management. “Fundamentals still broadly stack up.” Read more

However, note that the default rate they talked about is historical default rate. It does not predict future defaults. In fact, historical default rate to future probability of default is what historical volatility to implied volatility. Just because the recent historical volatility is low it does not mean that the volatility risk is low. This applies to the credit market too.

 

But default rates aren’t the only thing credit investors care about. Spreads have widened to levels not seen for more than a year as concerns grow of overheating in the U.S. market, trade disputes, rising rates, inflation and the end of the European Central Bank’s bond-buying program.

… The credit market may also be downplaying the potential impact of tariffs, analysts at UBS Group AG wrote in a July 24 report. They say investors should be cautious about sectors including tech, industrials, metals and mining. Higher corporate leverage may also lead to an increase in stress among non-cyclical industries such as consumer staples and healthcare, the analysts including Bhanu Baweja wrote.

…The end of loose monetary policies may also boost defaults in emerging markets next year, according to Abdul Kadir Hussain, the head of fixed income at Arqaam Capital, a Dubai-based investment bank.

ByMarketNews